Graph - Minimal Spanning Tree
Alogrithm :
Definition:-
A tree is a connected graph without cycles.
Properties of Trees
° A graph is a tree if and only if there is one and only one path joining any two of its vertices.
° A connected graph is a tree if and only if every one of its edges is a bridge.
° A connected graph is a tree if and only if it has N vertices and N; 1 edges.
Definitions:- ° A subgraph that spans (reaches out to ) all vertices of a graph is called a spanning subgraph.
° A subgraph that is a tree and that spans (reaches out to ) all vertices of the original graph is called a spanning tree.
° Among all the spanning trees of a weighted and connected graph, the one (possibly more) with the least total weight is called a minimum spanning tree (MST).
Find the minimal spanning tree for this G graph below by algorithm below
Example :
 |
| Graph G |
.We have Graph : V(G) = {V1,V2,V3,V4,V5,V6}V1 = 0 , V2 = 1 , V3 = 2 , V4 = 3 , V5 = 4 , V6 = 5
1.V(T) = { V1 }
2.V(E) = null
3.for i=1 to 6 then
.(i=1) 3.1 minWeight = inf
. 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? yes
. T 7 inf
. endVertex = V2
. edge = (V1,V2)
. minWeight = 7
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? yes
. T 3 7
. endVertex = V3
. edge = (V1,V3)
. minWeight = 3
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. T inf 3
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. T inf 3
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. T inf 3
. (j=2) if V2 in T ? no
. (j=3) if V3 in T ? no
. (j=4) if V4 in T ? no
. (j=5) if V5 in T ? no
. (j=6) if V6 in T ? no
. 3.3 V(T) = {V1} or {V3} ={V1,V3}
. 3.4 E(T) = {} or {(V1,V3)} = {(V1,V3)}
.(i=2) 3.1 minWeight = inf
. 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? yes
. T 7 inf
. endVertex = V2
. edge = (V1,V2)
. minWeight = 7
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? no
. F 3 7
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. T inf 7
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. T inf 7
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. T inf 7
. (j=2) if V2 in T ? no
. (j=3) if V3 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V3,V1) < minWeight ? no
. F 3 7
. (k=2) if V2 not in T && w(V3,V2) < minWeight ? no
. T inf 7
. (k=3) if V3 not in T && w(V3,V3) < minWeight ? no
. F inf 7
. (k=4) if V4 not in T && w(V3,V4) < minWeight ? no
. T inf 7
. (k=5) if V5 not in T && w(V3,V5) < minWeight ? no
. T 8 7
. (k=6) if V6 not in T && w(V3,V6) < minWeight ? yes
. T 1 7
. endVertex = V6
. edge = (V3,V6)
. minWeight = 1
. (j=4) if V4 in T ? no
. (j=5) if V5 in T ? no
. (j=6) if V6 in T ? no
. 3.3 V(T) = {V1,V3} or {V6} ={V1,V3,V6}
. 3.4 E(T) = {(V1,V3)} or {(V3,V6)} = {(V1,V3),(V3,V6)}
.(i=3) 3.1 minWeight = inf
. 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? yes
. T 7 inf
. endVertex = V2
. edge = (V1,V2)
. minWeight = 7
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? no
. F 3 7
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. T inf 7
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. T inf 7
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. F inf 7
. (j=2) if V2 in T ? no
. (j=3) if V3 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V3,V1) < minWeight ? no
. F 3 7
. (k=2) if V2 not in T && w(V3,V2) < minWeight ? no
. T inf 7
. (k=3) if V3 not in T && w(V3,V3) < minWeight ? no
. F inf 7
. (k=4) if V4 not in T && w(V3,V4) < minWeight ? no
. T inf 7
. (k=5) if V5 not in T && w(V3,V5) < minWeight ? no
. T 8 7
. (k=6) if V6 not in T && w(V3,V6) < minWeight ? no
. F 1 7
. (j=4) if V4 in T ? no
. (j=5) if V5 in T ? no
. (j=6) if V6 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V6,V1) < minWeight ? no
. F inf 7
. (k=2) if V2 not in T && w(V6,V2) < minWeight ? yes
. T 2 7
. endVertex = V2
. edge = (V6,V2)
. minWeight = 2
. (k=3) if V3 not in T && w(V6,V3) < minWeight ? no
. F 1 2
. (k=4) if V4 not in T && w(V6,V4) < minWeight ? no
. T inf 2
. (k=5) if V5 not in T && w(V6,V5) < minWeight ? no
. T 3 2
. (k=6) if V6 not in T && w(V6,V6) < minWeight ? no
. F inf 2
. 3.3 V(T) = {V1,V3,V6} or {V2} ={V1,V3,V6,V2}
. 3.4 E(T) = {(V1,V3),(V3,V6)} or {(V6,V2)} = {(V1,V3),(V3,V6),(V6,V2)}
.(i=4) 3.1 minWeight = inf
. 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? no
. F 7 inf
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? no
. F 3 inf
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. T inf inf
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. T inf inf
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. F inf inf
. (j=2) if V2 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V2,V1) < minWeight ? no
. F 7 inf
. (k=2) if V2 not in T && w(V2,V2) < minWeight ? no
. F inf inf
. (k=3) if V3 not in T && w(V2,V3) < minWeight ? no
. F inf inf
. (k=4) if V4 not in T && w(V2,V4) < minWeight ? yes
. T 5 inf
. endVertex = V4
. edge = (V2,V4)
. minWeight = 5
. (k=5) if V5 not in T && w(V2,V5) < minWeight ? no
. T inf 5
. (k=6) if V6 not in T && w(V2,V6) < minWeight ? no
. F 2 5
. (j=3) if V3 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V3,V1) < minWeight ? no
. F 3 5
. (k=2) if V2 not in T && w(V3,V2) < minWeight ? no
. F inf 5
. (k=3) if V3 not in T && w(V3,V3) < minWeight ? no
. F inf 5
. (k=4) if V4 not in T && w(V3,V4) < minWeight ? no
. T inf in5
. (k=5) if V5 not in T && w(V3,V5) < minWeight ? no
. T 8 5
. (k=6) if V6 not in T && w(V3,V6) < minWeight ? no
. F 1 5
. (j=4) if V4 in T ? no
. (j=5) if V5 in T ? no
. (j=6) if V6 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V6,V1) < minWeight ? no
. F inf 5
. (k=2) if V2 not in T && w(V6,V2) < minWeight ? no
. F 2 5
. (k=3) if V3 not in T && w(V6,V3) < minWeight ? no
. F 1 5
. (k=4) if V4 not in T && w(V6,V4) < minWeight ? no
. T inf 5
. (k=5) if V5 not in T && w(V6,V5) < minWeight ? no
. T 3 5
. endVertex = V5
. edge = (V6,V5)
. minWeight = 3
. (k=6) if V6 not in T && w(V6,V6) < minWeight ? no
. F inf 3
. 3.3 V(T) = {V1,V3,V6,V2} or {V5} ={V1,V3,V6,V2,V5}
. 3.4 E(T) = {(V1,V3),(V3,V6),(V6,V2)} or {(V6,V5)} = {(V1,V3),(V3,V6),(V6,V2),(V6,V5)} .(i=5) 3.1 minWeight = inf . 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? no
. F 7 inf
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? no
. F 3 inf
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. T inf inf
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. F inf inf
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. F inf inf
. (j=2) if V2 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V2,V1) < minWeight ? no
. F 7 inf
. (k=2) if V2 not in T && w(V2,V2) < minWeight ? no
. F inf inf
. (k=3) if V3 not in T && w(V2,V3) < minWeight ? no
. F inf inf
. (k=4) if V4 not in T && w(V2,V4) < minWeight ? yes
. T 5 inf
. endVertex = V4
. edge = (V2,V4)
. minWeight = 5
. (k=5) if V5 not in T && w(V2,V5) < minWeight ? no
. F inf 5
. (k=6) if V6 not in T && w(V2,V6) < minWeight ? no
. F 2 5
. (j=3) if V3 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V3,V1) < minWeight ? no
. F 3 5
. (k=2) if V2 not in T && w(V3,V2) < minWeight ? no
. F inf 5
. (k=3) if V3 not in T && w(V3,V3) < minWeight ? no
. F inf 5
. (k=4) if V4 not in T && w(V3,V4) < minWeight ? no
. T inf 5
. (k=5) if V5 not in T && w(V3,V5) < minWeight ? no
. F 8 5
. (k=6) if V6 not in T && w(V3,V6) < minWeight ? no
. F 1 5
. (j=4) if V4 in T ? no
. (j=5) if V5 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V5,V1) < minWeight ? no
. F inf 5
. (k=2) if V2 not in T && w(V5,V2) < minWeight ? no
. F inf 5
. (k=3) if V3 not in T && w(V5,V3) < minWeight ? no
. F 8 5
. (k=4) if V4 not in T && w(V5,V4) < minWeight ? no
. T 5 5
. (k=5) if V5 not in T && w(V5,V5) < minWeight ? no
. F inf 5
. (k=6) if V6 not in T && w(V5,V6) < minWeight ? no
. F 3 5
. (j=6) if V6 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V6,V1) < minWeight ? no
. F inf 5
. (k=2) if V2 not in T && w(V6,V2) < minWeight ? no
. F 2 5
. (k=3) if V3 not in T && w(V6,V3) < minWeight ? no
. F 1 5
. (k=4) if V4 not in T && w(V6,V4) < minWeight ? no
. T inf 5
. (k=5) if V5 not in T && w(V6,V5) < minWeight ? no
. F 3 5
. (k=6) if V6 not in T && w(V6,V6) < minWeight ? no
. F inf 5
. 3.3 V(T) = {V1,V3,V6,V2,V5} or {V4} ={V1,V3,V6,V2,V5,V4}
. 3.4 E(T) = {(V1,V3),(V3,V6),(V6,V2),(V6,V5)} or {(V2,V4)} = {(V1,V3),(V3,V6),(V6,V2),(V6,V5),(V2,V4)}.(i=6) 3.1 minWeight = inf
. 3.2 for j=1 to 6 then
. (j=1) if V1 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V1,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V1,V2) < minWeight ? no
. F 7 inf
. (k=3) if V3 not in T && w(V1,V3) < minWeight ? no
. F 3 inf
. (k=4) if V4 not in T && w(V1,V4) < minWeight ? no
. F inf inf
. (k=5) if V5 not in T && w(V1,V5) < minWeight ? no
. F inf inf
. (k=6) if V6 not in T && w(V1,V6) < minWeight ? no
. F inf inf
. (j=2) if V2 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V2,V1) < minWeight ? no
. F 7 inf
. (k=2) if V2 not in T && w(V2,V2) < minWeight ? no
. F inf inf
. (k=3) if V3 not in T && w(V2,V3) < minWeight ? no
. F inf inf
. (k=4) if V4 not in T && w(V2,V4) < minWeight ? no
. F 5 inf
. (k=5) if V5 not in T && w(V2,V5) < minWeight ? no
. F inf inf
. (k=6) if V6 not in T && w(V2,V6) < minWeight ? no
. F 2 inf
. (j=3) if V3 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V3,V1) < minWeight ? no
. F 3 7
. (k=2) if V2 not in T && w(V3,V2) < minWeight ? no
. F inf 7
. (k=3) if V3 not in T && w(V3,V3) < minWeight ? no
. F inf inf
. (k=4) if V4 not in T && w(V3,V4) < minWeight ? no
. F inf inf
. (k=5) if V5 not in T && w(V3,V5) < minWeight ? no
. F 8 inf
. (k=6) if V6 not in T && w(V3,V6) < minWeight ? no
. F 1 inf
. (j=4) if V4 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V4,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V4,V2) < minWeight ? no
. F 5 inf
. (k=3) if V3 not in T && w(V4,V3) < minWeight ? no
. F inf inf
. (k=4) if V4 not in T && w(V4,V4) < minWeight ? no
. F inf inf
. (k=5) if V5 not in T && w(V4,V5) < minWeight ? no
. F 5 inf
. (k=6) if V6 not in T && w(V4,V6) < minWeight ? no
. F inf inf
. (j=5) if V5 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V5,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V5,V2) < minWeight ? no
. F inf inf
. (k=3) if V3 not in T && w(V5,V3) < minWeight ? no
. F 8 inf
. (k=4) if V4 not in T && w(V5,V4) < minWeight ? no
. F 5 inf
. (k=5) if V5 not in T && w(V5,V5) < minWeight ? no
. F inf inf
. (k=6) if V6 not in T && w(V5,V6) < minWeight ? no
. F 3 inf
. (j=6) if V6 in T ? yes
. for k=1 to 6 then
. (k=1) if V1 not in T && w(V6,V1) < minWeight ? no
. F inf inf
. (k=2) if V2 not in T && w(V6,V2) < minWeight ? no
. F 2 inf
. (k=3) if V3 not in T && w(V6,V3) < minWeight ? no
. F 1 inf
. (k=4) if V4 not in T && w(V6,V4) < minWeight ? no
. F inf inf
. (k=5) if V5 not in T && w(V6,V5) < minWeight ? no
. F 3 inf
. (k=6) if V6 not in T && w(V6,V6) < minWeight ? no
. F inf inf
. 3.3 V(T) = {V1,V3,V6,V2,V5,V4} or {V4} ={V1,V3,V6,V2,V5,V4}
. 3.4 E(T) = {(V1,V3),(V3,V6),(V6,V2),(V6,V5),(V2,V4)} or {(V2,V4)} = {(V1,V3),(V3,V6),(V6,V2),(V6,V5),(V2,V4)}
 |
| Red edge will be the minimal spanning tree for Graph G |
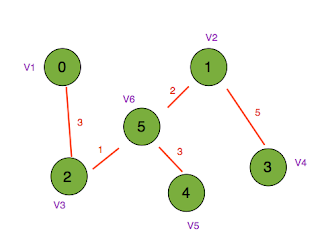 |
| Minimal Spanning Tree T |
No comments:
Post a Comment