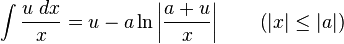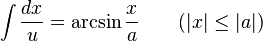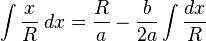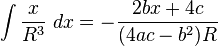Integrals involving 
[edit] Integrals involving 
Assume (x2 > a2), for (x2 < a2), see next section:
Here  , where the positive value of
, where the positive value of  is to be taken.
is to be taken.
m\ge0\mbox{)}" src="http://upload.wikimedia.org/math/7/e/c/7ec61e0b86221a7e14575832d055c1d9.png">
[edit] Integrals involving 
[edit] Integrals involving 
Assume (ax2 + bx + c) cannot be reduced to the following expression (px + q)2 for some p and q.
0\mbox{)}" src="http://upload.wikimedia.org/math/b/9/7/b9786694b8364705405868b754f3e73a.png">
0\mbox{, }4ac-b^2>0\mbox{)}" src="http://upload.wikimedia.org/math/0/d/6/0d6ddd4644254d630d3993720801c6ad.png">
0\mbox{, }4ac-b^2=0\mbox{)}" src="http://upload.wikimedia.org/math/6/c/f/6cfab7115ce8ce8a82a1d238a1a80b7b.png">
[edit] Integrals involving 
0, \quad a x > 0\mbox{)} \\ -\frac{2}{\sqrt{b}} \mathrm{artanh}\left( \frac{S}{\sqrt{b}}\right) & \mbox{(for }b > 0, \quad a x < src="http://upload.wikimedia.org/math/1/e/b/1ebd0028aa19fcf88af1c1ac87e293b9.png">
0, \quad a x > 0\mbox{)} \\ 2 \left( S - \sqrt{b}\,\mathrm{artanh}\left( \frac{S}{\sqrt{b}}\right)\right) & \mbox{(for }b > 0, \quad a x < src="http://upload.wikimedia.org/math/6/1/2/612fd00fa1ae63401b55deaa24ee002f.png">






































![\int\frac{dx}{s^5}=\frac{1}{a^4}\left[\frac{x}{s}-\frac{1}{3}\frac{x^3}{s^3}\right]](http://upload.wikimedia.org/math/9/7/6/976ffe1b77aeafaba971eee9d6a05163.png)
![\int\frac{dx}{s^7} =-\frac{1}{a^6}\left[\frac{x}{s}-\frac{2}{3}\frac{x^3}{s^3}+\frac{1}{5}\frac{x^5}{s^5}\right]](http://upload.wikimedia.org/math/d/8/c/d8c21f20257e0ca63e5c22e228f30ac7.png)
![\int\frac{dx}{s^9} =\frac{1}{a^8}\left[\frac{x}{s}-\frac{3}{3}\frac{x^3}{s^3}+\frac{3}{5}\frac{x^5}{s^5}-\frac{1}{7}\frac{x^7}{s^7}\right]](http://upload.wikimedia.org/math/f/c/a/fcaa9b35840c23cf8e54ef1a46bf39b9.png)
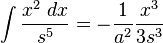
![\int\frac{x^2\;dx}{s^7} = \frac{1}{a^4}\left[\frac{1}{3}\frac{x^3}{s^3}-\frac{1}{5}\frac{x^5}{s^5}\right]](http://upload.wikimedia.org/math/1/0/d/10d9eca1dd15754f7b6c8cd4a66aa8bf.png)
![\int\frac{x^2\;dx}{s^9} = -\frac{1}{a^6}\left[\frac{1}{3}\frac{x^3}{s^3}-\frac{2}{5}\frac{x^5}{s^5}+\frac{1}{7}\frac{x^7}{s^7}\right]](http://upload.wikimedia.org/math/5/4/c/54c28b6ef015b425f44119203c27e5be.png)